
Zie ook de annotaties bij de toets 3F cito_voorbeeldtoets_3F.htm
Cito webpagina voorbeeldtoetsen
College voor Examens (maart 2012). Implementatie referentieniveaus taal en rekenen in eindexamen vo. pdf
(26-9-2013). Aanbieding voortgangsrapportage invoering referentieniveaus taal en rekenen 2013 html
(31-5-2013). Prestaties basisonderwijs taal en rekenen 2012 (CITO). html
Voor een kritische analyse van toetsen zoals deze voorbeeldrekentoets-3F als beoogd onderdeel van eindexamens zie Henk Pfaltzgraff, Joost Hulshof en Ben Wilbrink hier]
De laatste dagen — in voorbereiding op een presentatie voor mijn oud-collega’s van het Kohnstamm Instituut — ben ik ervan overtuigd geraakt dat de concrete vragen in de Cito-voorbeeldrekentoets-3F de beste illustratie vormen van het probleem waarmee Nederland nu zit opgescheept. Nu wil het geval dat in de allereerste vraag al een groot aantal pijnpunten aanwezig zijn: analyse van de kunstfouten bij deze eerste vraag kan dus volstaan.
Hoe het er vroeger aan toeging: zie Turkstra, in Euclides 1957. Een ware tijdcapsule: Turkstra presenteert daar een toets technisch rekenen, en een test op denkvermogen aan de hand van rekenopgaven (onderdelen van een toelatingsexamen), plus de scores, en rapportcijfers, van de toegelaten leerlingen. Ik heb de scans hier staan: zie hier [for the time being: ook als bijlage onderaan deze pagina]
Ik beschouw deze vraag 1 niet als een beroerd buitenbeentje in deze rekentoets, eerder als representatief voor wat men bij het Cito onder rekentoetsopgaven verstaat.

1. Het gebruik van illustraties is niet onschuldig. Het belast het werkgeheugen en kan daardoor sommige kandidaten meer in problemen brengen dan andere. Dat mag gewoon niet gebeuren in een toets als deze, onderdeel van een examen. Erger nog: de spelregels van het examen zijn dat de kandidaat goed moet lezen — in dit geval dus ók irrelevante informatie in de afbeelding, en dat is heel wat, terwijl de vraag zónder deze afbeelding is te beantwoorden (met een paar kleine tekstwijzigingen)!
Inez E. Berends & Ernest C.D.M. van Lieshout (2009). The effect of illustrations in arithmetic problem-solving: Effects of increased cognitive load. Learning and Instruction 19 (2009) 345-353.
http://dspace.ubvu.vu.nl/bitstream/handle/1871/34321/222375.pdf
2. Een richtlijn voor het ontwerpen van examenvragen is dat alle benodigde informatie in de stam van de vraag staat, als dat maar enigszins mogelijk is. In vraag 1 is daar niet aan voldaan omdat de kandidaat gedwongen is de afbeelding te bestuderen op de informatie die daarin is gegeven. In dit geval is bestuderen van de afbeelding nodig om de dubbelzinnigheid van prijs, prijzen, lotnummer, en 1/5 lot op te lossen.
3. Zeker in een rekentoets moet alles wat met het rekenen zelf te maken kan hebben, op orde zijn. De juiste spelling is hier volkomen zoek: ‘twee en een half’ is geen Nederlands, want het moet zijn: tweeënhalf. Wat ook mag: tweeëneenhalf. [bron: Van Dale Spelling 2005; Stijlboek NRC Handelsblad 2000] Maar daarmee is de zaak nog niet op orde: wanneer een exact bedrag is bedoeld, moet het in cijfers worden geschreven: 2,5 miljoen; zo niet, dan is een globaal bedrag bedoeld, en zijn alleen de eerste twee cijfers significant. Voor deze opgave is dat van cruciaal belang, omdat de tweede prijs een verwaarloosbaar bedrag is tegenover die tweeëneenhalf miljoen.
‘1⁄5 lot’ schrijven we als ‘1⁄5e lot’. Schrijven we voor NRC Handelsblad, dan is het ‘eenvijfde lot’, en als het in cijfers moet, dan liever ‘0,2’ schrijven dan ‘1⁄5e’ [Stijlboek NRC Handelsblad lemma breuken] Maar in het geval van 1⁄5e loten ziet 0,2 er onnatuurlijk uit.
Na al het voorgaande is het duidelijk dat de ontwerper van deze vraag er een potje van heeft gemaakt door de ene keer een bedrag voluit te schrijven, en de andere keer in cijfers. Nu zal geen enkele leerling hierbij de vinger opsteken en protesteren, maar deze slordigheid zorgt er wel voor dat de tekst lastiger is te lezen en te interpreteren.
4. Uiteraard moet de tekst van een examenvraag goed Nederlands zijn. Niet omdat het zo zou horen, maar om dubbelzinnigheden zoveel mogelijk uit te sluiten.
Evers-Vermeul, J. & Land, J. (2012). Slecht gelezen of slecht geleerd? (aflevering 2). Examens, Tijdschrift voor de toetspraktijk, 9(2), 25-29.
5. wereldkennis
Het is onvermijdelijk dat in een rekentoets waarin uitvoerige contexten worden ingezet, aanspraak wordt gedaan op de wereldkennis van de kandidaten. Maar de toets mag natuurlijk niet een toets op wereldkennis worden: de kennis waar aanspraak op wordt gedaan, moet bij alle kandidaten in gelijke mate en wel probleemloos beschikbaar zijn. In het geval van loten en 1⁄5e delen daarvan, is aan die eis niet voldaan. De context zal ongetwijfeld veel kandidaten voor een verrassing plaatsen: 1⁄5e lot, wat is dat?
6. contexten
Hier ligt een enorm probleem, want wat zijn nu de typische contexten waarin kandidaten ‘functioneel’ zouden moeten kunnen rekenen? Hier is natuurlijk geen goed antwoord op, tenzij we genoegen nemen met boodschappen doen bij de grootgrutter. In dit geval hebben we een idiote context: een hoofdprijs in een grote loterij winnen.
Dit contextprobleem ligt anders wanneer het zou gaan om een rekentoets voor een specifieke beroepsgroep, zoals verpleegkundigen. Welnu, het Cito heeft een dergelijke rekentoets in ontwikkeling, interessant onderzoek (pilots): 80% van verpleegkundigen uit de beroepspraktijk scoort ‘onvoldoende’.
7. rekenmachine
Hier mag een rekenmachine bij worden gebruikt. Dit is testtechnisch van de gekke, want het maakt de scores op deze vraag (op de rekentoets) oninterpreteerbaar als het gaat om de vraag os deze kandidaten rekenvaardig zijn. Dat is simpele testpsychologie. Hierachter ligt een politiek spel,
De taal: daar deugt niet veel van.
Waarom krijgt de leerling voor deze opgave de beschikking over een rekenmachine?
Is dit (kerndoel) hoofdrekenen? -->
H. Turkstra (1957). Een onderzoek over de correlatie tussen de vorderingen voor algebra en meetkunde in de eerste klas van de middelbare school en het cijfer voor rekenen op de l.s. en op het toelatingsexamen voor de middelbare school. Euclides, 32, 161-172.
Ik zal uit dit artikel van Turkstra de relevante informatie over de in de vijftiger jaren gebruikte rekentoetsen overnemen (o.a. toelatingsexamen rekenen 1955 Hilversum). Waarschijnlijk zal blijken dat een deel van de verwarring over het rekenen kennelijk van alle tijden is (‘leren denken’, samenhang met verschillen in intelligentie).
De laatste van de serie scans hierbeneden geeft voor een enkele klas leerlingen de cijfers die zij voor rekenen op hun laatste rapport van de lagere school hadden. Aan die cijfers is te zien dat deze klas een topselectie uit de Hilversumse leerlingen vormen. Laten we zeggen dat deze leerlingen behoren tot de top 15% van de 12 jarigen. Dit gegeven is niet onbelangrijk voor de interpretatie van de onderzoekgegevens van Turkstra. In diezelfde scan ook de scores voor respectievelijk deel I en II van de toelatingstoets rekenen. Deel I is een toets op wat Turkstra ‘technisch’ rekenen noemt; met een beetje fantasie zou je kunnen zeggen dat Turkstra hier een rekentoets op niveau 3S heeft gemaakt. Ik ben benieuwd of Jan van de Craats, voorzitter van de commissie-3S, aan kan geven welke interessante verschillen en overeenkomsten hij ziet. De uitslagen op deze rekentoets I geven enig houvast. Ik neem aan dat het cijfer voor deze rekentoets I gelijk is aan het aantal goed beantwoorde opgaven. [Dit is een malle regel, die als enig voordeel heeft dat iedereen weet waar hij of zij aan toe is. Psychometrici zullen ook als voordeel zien dat zodoende de scores goed spreiden, maar of dat verdedigbaar onderwijsbeleid is, waag ik aan te vechten. B.W.]


Rekentoets II is niet een toets met traditionele redactiesommen. Evenmin zijn het contextopgaven avant la lettre. Deze opgaven zijn bedoeld om de intelligentie van de leerlingen te testen. Het is interessant om een studie van dit testje te maken, in vergelijking met sommige opgaven uit de voorbeeldrekentoetsen van het Cito/CvE, en bedenk dan dat de scores op dit testje (in de laatste scan gegeven) afkomstig zijn van een topgroep van ca. 15% uit de bevolking van twaalfjarigen. Merk op dat de rekentest I met hoge scores wordt gemaakt, en dat er op de intelligentietest II een grote spreiding van scores is. Daar valt heel wat over te filosoferen, maar dat zal ik hier niet doen, anders dan de filosofie van Turkstra en anderen kort uitleggen.

Opgave 5 is een algebrasom. Althans, ik zie niet in hoe deze valt uit te rekenen anders dan door algebraïsch te redeneren (voorbeeld van de regel dat deklen door een breuk gelijk staat aan het vermenigvuldigen met het omgekeerde va die breuk). Voor de oorlog is er een pittige discussie geweest over redactiesommen die veel beter algebraïsch zijn op te lossen dan door ze uit te rekenen: doe dat dan ook algebraïsch, in het lager onderwijs (voorstel van o.a. Philip Kohnstamm, als ik me goed herinner).

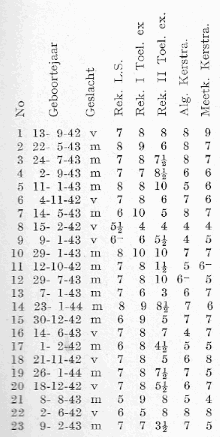
Het is wel grappig om te zien hoe Turkstra worstelt met de gegevens die hij in de eigen school in een reeks klassen heeft verzameld. Hij noemt het correlatieonderzoek, maar hij berekent werkelijk geen enkele correlatie. Geweldig zinvol is heel zijn exercitie op voorhand al niet, als het hem erom is te doen voor de groep toegelaten leerlingen de wiskundeprestaties te voorspellen op basis van de scores op zijn tests Rekenen I en Rekenen II. Hij zit met zijn data opgesloten binnen een selecte en geselecteerde groep leerlingen: daarbinnen zijn de correlaties niet hoog door de restriction of range die het gevolg is van de zelf-selectie van de kandidaten, en de selectie binnen de groep kandidaten. Wie de validiteit van een selectietest wil leren kennen, moet dat in beginsel onderzoeken binnen een niet-geselecteerde groep. Als we de zelf-selectie buiten beschouwing laten, dus de groep aanmelders voor de toelatingsselectie als uitgangspunt nemen, dan doe je zo’n onderzoek door een keer de hele aangemelde groep zowel te testen (en de resultaten daarvan geheim te houden bij een notaris) als de hele groep toe te laten. En dan zien hoe de balletjes gaan rollen. In de 19e eeuw was er een prachtige kans, die niet benut is: in de eerste jaren van de HBS van Thorbecke was er geen toelatingsselectie.
Allemaal gekheid, natuurlijk. Wat wel serieus is: dat wiskundigen altijd maar weer flirten met de ‘denkpschologie’, en vervolgens daar vreemde dingen mee gaan doen. Turkstra doet het. Pierre van Hiele doet het (zie NAW juni 2012), Freudenthal en heel zijn groep doen het. Niemand komt op het idee om de psychologie van het reken- en wiskundeonderwijs te beleggen waar ze thuishoort: bij psychologen.
Concreet. Als je verschillen in intelligentie wilt testen, doe dat dan niet met een Rekentest II die de indruk wekt over rekenen te gaan. Gebruik een intelligentietest. Noem desnoods je test met rekenproblemen ‘intelligentietest’.
De actualiteit van deze thematiek is natuurlijk dat niet alleen de voorbeeldrekentoetsen wemelen van de kenmerken die wijzen op meting van verschillen in intelligentie (werkgeheugen, zie ook hierbeneden), maar dat er in het rekenwereldje nog steeds bij voorkeur wordt gesproken over ‘begrijpen, inzicht en probleemoplossen’, wat categorieën zijn die beter passen bij intelligentietesterij dan bij het rekenonderwijs.
Rekenen I ( . . . ) is eigenlijk een toets, dat iedere candidaat eenvoudig technisch rekenwerk vlot kan verrichten, kan hoofdrekenen met niet te grote getallen en nauwkeurig kan cijferen. Het is de minimumeis, die men kan en mag stellen. Zonder deze kennis en vaardigheid kan men eenvoudig geen wiskunde in klas 1 van de M.S. beoefenen. Maar het examen moet meer inhouden dan enkel een toetsing van de techniek der verworven kennis.
Vandaar dat in Rekenen II een onderzoek wordt ingesteld naar het logisch en zinvol inzien van het verband tussen de beschikbare gegevens in eenvoudige denkvraagstukken. De candidaat moet zich weten te redden met opgaven, waarin gevallen en situaties voorkomen, die hij nog niet eerder is tegengekomen, waarop hij ook niet kan worden afgericht. Daartoe dienden, zoals we in par. 1 zagen, het soort opgaven als tot nu toe door het Nutsseminarium werden opgesteld. Echter eenvoudige opgaven, die een appèl doen op het ordenend vermogen, het combinatievermogen, het critisch inzicht e.d. In par. 91 van onze Rekendidactiek [Turkstra & Timmer. B.W.] somden wij er een aantal hele eenvoudige op (minimumeis), waarvan ik er enkele hier weergeef:
2 20 52 3 30 ..
| Jan | Piet | Kees | Henk | Arie | Wim
jaren ..| 12 | 13 | 14 | 15 | 16 | 17
kg . . .| 42 | 47 | 48 | 52 | 54 | 60
Zet op een horizontale lijn vanuit een bepaald beginpunt de jaren naar rechts uit en vanuit hetzelfde punt op een verticale lijn de kg naar boven. Welke van deze jongens is de lichtste? Welke is voor zijn leeftijd de lichtste? Welke is de zwaarste? Welke is voor zijn leeftijd de zwaarste? (dit komt dus neer op een eenvoudige grafiek kunnen lezen).
Het correct oplossen van dit soort vraagstukjes vordert naast een beheerste rekentechniek ook een critisch inzicht en een zeker ordenend vermogen. En dat juist hebben we nodig bij ons wiskundeonderwijs in de eerste klas van de M.S.
Turkstra, 1957, p. 164-165.
De straks genoemde Toelatingscommissie had in 1929 behalve de traditionele ook enkele z.g. ‘ongewone’ vraagstukken opgegeven en ze heeft nagegaan hoe het verloop der vorderingen voor wiskunde was van die candidaten, die deze afwijkende vraagstukken (waarop de candidaten dus niet waren afgericht) goed hadden opgelost. Het bleek, zo rapporteert de commissie, dat deze over ’t algemeen goede leerlingen voor het vak wiskunde waren.
Ook in de volgende jaren heeft men dergelijke proeven gedaan, nu eens met minder dan met meer succes. Door deze resultaten gestimuleerd, kwam in het najaar van 1983, door ovrleg van de wiskundegroep van de W.V.O. (werkgemeenschap voor vernieuwing van Opvoeding en Onderwijs) en het Nutsseminarium voor Paedagogiek, een wiskundewerkgroep tot stand, onder leiding van Prof. Kohnstamm, die zich ten doel stelde vragen van wiskunde-didactiek, in ’t bijzonder betrekking hadden op de aansluiting L.O.—M.O., te onderzoeken. Deze commissie, waarin vertegenwoordigers van het L.O. en van het M.O. zitting hadden, heeft sindsdien de taak toebedeeld gekregen om elk jaar rekenopgaven voor het toelatingsexamen op te stellen, de U bekende Rekenopgaven van het Nutsseminarium. Als medewerker in deze commissie heb ik van nabij mogen kennis nemen van de nieuwe inzichten, volgens welk de commissie zich laat leiden. Getracht wordt n.l. op de grondslag van de psychologie van het denken (denkpsychologische school), speciaal van het mathematische denken, opgaven op te stellen, die afwijken van het oude type ‘denksommen’. Men zal in deze opgaven dan ook niet aantreffen de bekende foefjes en handigheidjes uit de oude denksommen, waarop nu eenmaal iedere leerling perfect kan wordenafgericht (appèl op het gehuegen) en die dus èn als selectiemiddel èn als intelligentietest ten enemale waardeloos zijn. Maar er wordt ernstig naar gestreefd, door dit werk bepaalde intelligentiecriteria, als b.v. het ordenen van de gegevens, combinatie van de juiste gegevens, selectie bij het overzien van de gegevens (ordenend vermogen, combinatievermogen, selectief vermogen ofwel critisch inzicht, enz.) te testen. Of ons dat elk jaar in voldoende mate is gelukt, is natuurlijk zeer de vraag.
Over de in 1948 door de candidaten gemaakte examenopgaven, heeft het Nutsseminarium een uitgebreid onderzoek ingesteld naar de correlatie met de rapportcijfers voor wiskunde en het gemiddelde rapportcijfer in de eerste klas en de uitslag van de overgang naar de tweede klas.
Dit onderzoek heeft niet opgeleverd wat wij er van hadden verwacht. Wel bleek over het algemeen, dat met dit werk de knappe en de domme leerlingen er vrij behoorlijk uit waren te halen, maar omtrent de grote middenmoot heeft het ons niet verder gebracht. [Heeft men zich werkelijk laten misleiden door de ana;yse niet behoorlijk statistisch uit te voeren? B.W.] Misschien lag het aan het feit, dat deze opgaven vaak te moeilijk waren gesteld, n.l. boven het kinderlijke bevattingsvermogen. Met het oog hierop is is de commissie de laatste jaren ertoe overgegaan om naast de stellen van 3 lange tekstopgaven ook stellen van 5 of meer kleinere opgaven, met enkelvoudige rekendenkelementen, op te stellen, zonder te vervallen in de traditionele oude denksommen van het genre weg-, werk- en kraansommen, waar de candidaten nu eenmaal perfect op kunnen worden afgericht.
Turkstra, 1957, p. 161-162.
Wat betreft de aard van het tegenwoordige rekenonderwijs op de L.S., daar is natuurlijk een artikel op zich zelf wel over te schrijven. Dat zou ons echter te ver voeren. Hoofdzaak is, dat wij weten, dathet rekenonderwijs op de L.S. de laatste jaren sterk invloed heeft ondervonden van de nieuwe inzichten in de rekendidactiek [en de realisten in de Freudenthal-groep maar roepen dat zij de eerste zijn die die de didactiek van het rekenonderwijs op de kaart hebben gezet. B.W.] Wie de moeite neemt om de nieuwe rekenmethodes, die op de L.S. gebruikt worden, eens aandachtig door te bladeren, zal het opvallen, dat de leerlingen een heel ander soort rekenen voorgezet krijgen dan b.v. een 20 jaar geleden. Geen weg-, werk- en kraansommen, geen onpractische levensvreemde vraagstukken, maar opgaven in de trant van:
het opstellen van schema’s uit opsommingen;
het invullen van open plaatsen in een schema;
het tekenen van een grafiek naar aanleiding van een gegeven schema of tabel;
het afronden van een onnauwkeurig antwoord;
het schatten en controleren van het antwoord en meer dergelijke rekencriteria en natuurlijk ook gewoon technisch rekenen.
Meer kan ik er in dit korte bestek niet over schrijven. Uitvoerig hebben we onze ideeën over een neiuwe rekendidactiek weergegeven in ons werk ‘Rekendidactiek in 2 delen, Turkstra en Timmer, uitg. Wolters, Groningen’.
Turkstra, 1957, p. 163-164.
Ik begin te vermoeden dat deze intelligentietest-achtige rekenopgaven wel eens resultaten kunnen geven die behoorlijk voorspelbaar zijn op basis van de kenmerken van het werkgeheugen van de betreffende leerlingen: heeft dat werkgeheugen wat meer capaciteit, dan is het meteen een stuk makkelijker om al die nieuwe informatie overzichtelijk op te nemen dan voor leerlingen bij wie dat werkgeheugen minder aankan. Zie voor een recente publicatie over dit fenomeen:
Carsten K. W. De Dreu, Bernard A. Nijstad, Matthijs Baas, Inge Wolsink and Marieke Roskes (2012). Working Memory Benefits Creative Insight, Musical Improvisation, and Original Ideation Through Maintained Task-Focused Attention. Personality and Social Psychology Bulletin, 38, 656. abstract
uit de conlucies:
Anecdotes and introspection suggest that creative geniuses benefitted from sustained attention and executive control, and a few systematic studies indeed revealed positive correlations between WMC and creative fluency—WMC associated with the generation of more creative solutions (e.g., Oberauer et al., 2008). Building on these works, the current study makes three contributions, namely (a) working memory not only predicts fluency but also the hallmark of creativity: insight performance and original ideation (Studies 1-4), (b) working memory relates to creative insight and ideation over and beyond general intelligence (Study 2), and (c) working memory relates to creativity because it enables persistence (i.e., sustained task-directed effort) rather than cognitive flexibility (Studies 2-4). These contributions have several implications for our thinking about creativity in general, and DPCM in particular. They also speak to a lingering issue in the literature on the benefits and detriments of conscious information processing and effortful deliberation.
Graeme Paton (17 Jan 2013). Children to be marked up for using long division in maths. The Telegraph html
Ministers have already announced that calculators will be banned in maths tests sat by 11-year-olds at the end of primary school.
Elizabeth Truss, the Education Minister, will outline the plans in a speech to the North of England Education Conference in Sheffield on Thursday.
Speaking before the address, she said: “Chunking and gridding are tortured techniques but they have become the norm in recent years. Children just end up repeatedly adding or subtracting numbers, and batches of numbers.
“They may give the right answer but they are not quick, efficient methods, nor are they methods children can build on, and apply to more complicated problems.
“Column methods of addition and subtraction, short and long multiplication and division are far simpler, far quicker, far more effective and allow children to understand properly the calculation and therefore move on to more advanced problems.”
The draft national curriculum for primary maths – published last year – specifies that children should learn “efficient calculation methods”, such as short and long multiplication and division.
![]() http://www.benwilbrink.nl/projecten/cito_staatsloterij_3F.htm
http://goo.gl/0juONi
http://www.benwilbrink.nl/projecten/cito_staatsloterij_3F.htm
http://goo.gl/0juONi